Epoka Średniowiecza jest powszechnie uważana za ciemny okres w dziejach ludzkości, w którym rozwój nauki, technologii i sztuki niemal się zatrzymał. Tak naprawdę te przekonania opierają się jednak wyłącznie na stereotypach. Rzeczywistość przedstawia się zgoła inaczej: w tym okresie wciąż rodzili się wielcy geniusze, ludzie nadal ciężko pracowali, rozwijali się, a świat wcale nie stanął w miejscu. Właśnie w tamtej epoce, około 1170 roku, urodził się Leonardo. Nie, nie Leonardo, którego wszyscy znają, da Vinci. Leonardo, o którym mowa to Pisano, znany także jako Fibonacci – drugi wielki włoski Leonardo, który przejdzie do historii, nawet o tym nie wiedząc, a to za sprawą… królików.
Leonardo Pisano, jak wskazuje nazwisko, przychodzi na świat w Pizie, która w XII wieku jest tętniącym sercem ówczesnego zachodniego świata. W tym czasie Włochy są najważniejszym ośrodkiem handlu między krajami basenu Morza Śródziemnego: średniowiecze średniowieczem, handel kwitnie. Leonardo urodził się więc, jak wielu innych pizańczyków w rodzinie kupieckiej, co zadecydowało o jego późniejszym losie. W wieku czternastu lat udaje się z ojcem do miasta Bidżaja, jednego z najlepiej prosperujących portów islamskich w owych czasach. W ten sposób mały Leonardo nie tylko zapoznaje się ze światem handlu, gdzie znaczenie mają umiejętności wykonywania skomplikowanych obliczeń i pomysłowość, ale wkracza w ten świat w sposób szczególny, przybywając do portu na styku dwóch kultur, tam spotykają się dwa światy: arabski i europejski. To miejsce na pograniczu, gdzie pojawiają się problemy „międzynarodowego” handlu, takie jak podatki importowe i eksportowe, ryzykowne operacje z pożyczkami i odsetkami, wymiana walut, zasób i wartość towarów, które zmieniają się dynamicznie z dnia na dzień. Prawdziwe piekło dla tych, którzy muszą stawić czoła całej złożoności funkcjonowania rynku międzynarodowego. Dla Leonarda, chłopaka o umyśle bardzo otwartym i gotowym do nauki, miejsce to okazuje się być prawdziwą kopalnią wiedzy i możliwości. Jest absolutnie zafascynowany mistrzostwem, jakie osiągnęli Arabowie w wykonywaniu nawet bardzo skomplikowanych obliczeń, przy użyciu liczb o dziwnej formie, tak różnej od tej, której używano wówczas w Europie.
Te liczby nie są zwykłymi cyframi rzymskimi takimi, jak I, X, V, L i tym podobne, ale przedstawiają się dziwacznie dla Europejczyka. Składają się z dziesięciu symboli, od 1 do 9 i dodatkowo wykorzystują jeszcze jeden przedziwny symbol oznaczający nic, zero. Umiejętnie dobierane, okazują się być bardzo potężnym narzędziem do obliczeń – Leonardo rozumie, że świat może się dzięki nim zmienić. Cyfry rzymskie, owszem zasłużone w historii ludzkości, dają mniej możliwości w porównaniu z cudami, które można robić z nowymi cyframi arabskimi. To właśnie poprzez badanie tych symboli i ich nieskończonych możliwości, Leonardo zaczyna stosować nowe rozwiązania obliczeniowe, najpierw w samym porcie Bidżaja, potem w innych miejscach. Wszystkie złożone problemy z cyframi rzymskimi okazują się mieć znacznie prostsze rozwiązania, jeśli podejść do nich z pomysłem przy pomocy tych dziwnych, innowacyjnych symboli arabskich. Leonardo Fibonacci staje się w ten sposób jednym z najzdolniejszych „ekspertów finansowych” ówczesnego świata i zaczyna rozwijać techniki radzenia sobie ze złożonością operacji handlowych. Musi jednak zmierzyć się w Europie z pierwszym problemem: zacząć od podstaw, próbować wyjaśnić innym, czym owe dziwne liczby są i jak mogą być używane.
W tym celu pisze księgę Liber Abaci, która praktycznie wywraca do góry nogami ówczesny świat finansów i jest uważana za kamień milowy w procesie wprowadzania matematyki w Europie. W rzeczywistości wielu zapomina, skąd w ogóle się wzięła owa księga i co tak naprawdę zawiera. Oczywiście Liber Abaci wyjaśnia nową matematykę, arabskie cyfry od 0 do 9 oraz przedstawia nowe, uniwersalne techniki obliczeniowe. Liczby dla Leonarda Fibonacciego, syna kupców, są jednak tylko środkiem, a nie celem samym w sobie, są narzędziem służącym do rozwiązywania złożoności naszego świata, a w szczególności świata handlu, towarów, finansów w życiu codziennym. Fibonacci zapisał się w historii właśnie ze względu na jeden z tych praktycznych problemów, które stawia przed sobą i rozwiązuje za pomocą cyfr arabskich.
Wielkim, choć niestety zapomnianym, dziedzictwem Fibonacciego jest w rzeczywistości wprowadzenie nowych technik obliczeniowych, które opracował, by lepiej i łatwiej stawiać czoła realnemu światu. Rozpoczyna tak naprawdę pierwszą wielką rewolucję finansową w zachodnim świecie europejskim. Dlatego też jego dzieło w tamtym czasie odnosi niesamowity sukces: poza niewątpliwymi walorami dydaktycznymi ma jeszcze inne: nie wyjaśnia liczb arabskich tylko w sposób teoretyczny, ale pokazuje, jak można je wykorzystać realnie, jak za ich pomocą tłumaczyć świat, analizować go. Jego nowa wiedza rozpowszechnia się szybko w Europie, a potem na całym świecie. Nawet jeśli to właśnie Fibonacci rozpoczął wielką rewolucję w liczbach, jego nazwisko, jako jednego z dawnych geniuszy matematycznych odeszłoby w zapomnienie, pozostało jedynie na kartach pisanych przez znawców historii. Świat potrafi zapominać. Leonardo Fibonacci przeszedł do historii powszechnej, trwającej tysiąclecia, z powodu tylko jednej z wielu praktycznych kwestii, które rozwiązał, a mianowicie problemu z królikami. Stosunkowo łatwego problemu w porównaniu z wieloma innymi, które opisuje w swoim wielkim matematycznym dziele.
Tu mamy jednak do czynienia z wyjątkowo ważnymi dla świata liczbami, które na zawsze będą nosić jego imię.
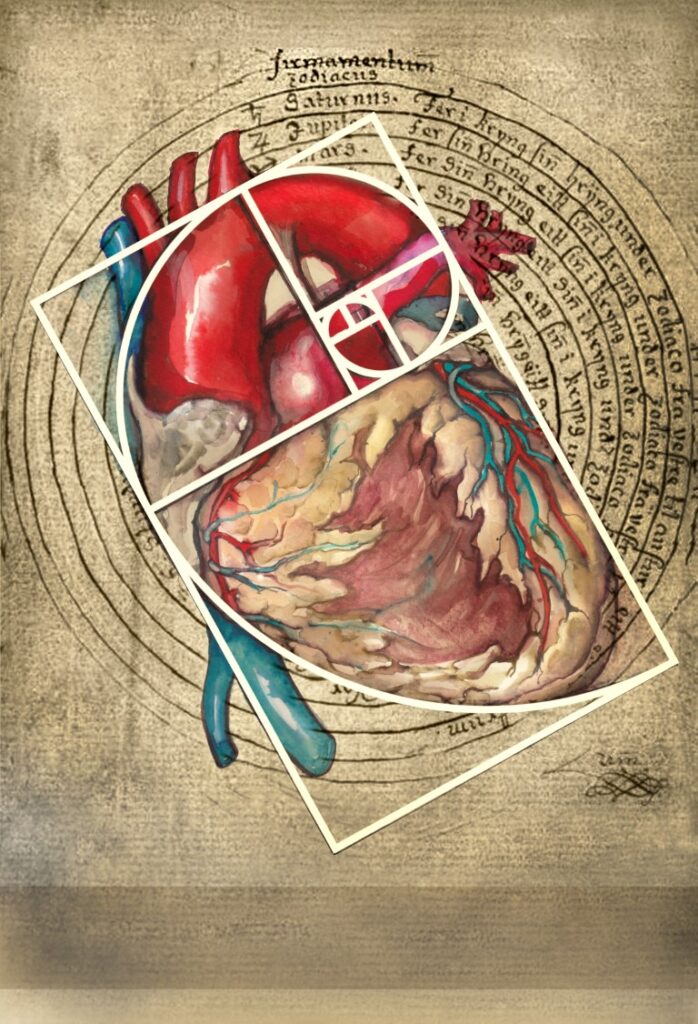
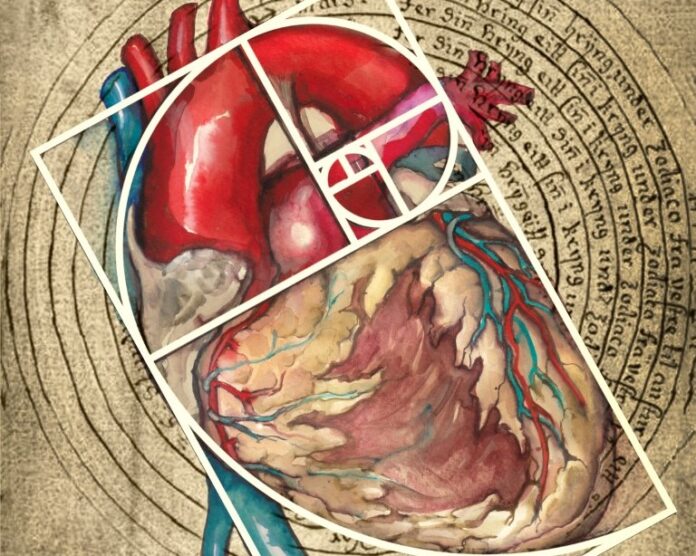
Sprawa dotyczy zatem królików i należy do grupy tych praktycznych problemów, które Fibonacci przedstawia, aby zobrazować potęgę i uniwersalność nowych cyfr arabskich. Poza problemami dotyczącymi podziału żywności, pieniędzy itp., Leonardo, jako syn kupca, omawia, w jaki sposób cyfry arabskie mogą byćużywane do obliczania tzw. towarów dynamicznych, czyli na przykład rozmnażających się zwierząt. Co się stanie, jeśli zainwestuję kupując parę królików i dam im się rozmnażać? Jak rozwinie się moja hodowla? Fibonacci analizuje ten problem za pomocą nowo poznanych cyfr i znajduje właściwy wzór matematyczny, który oblicza, jak hodowla rozwija się z pokolenia na pokolenie. Jej wielkość, jak pokazuje Fibonacci, rośnie w określony sposób, mierzony w parach królików: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 i tak dalej. Fibonacci pokazuje, że populacja pomnaża się w łatwy do obliczenia sposób: wystarczy dodać dwie kolejne liczby z sekwencji, aby otrzymać następną w ciągu. Liczby te stały się tak sławne, że przyjęły odtąd nazwę liczb Fibonacciego. Dlaczego spośród wszystkich rozwiązywanych w księdze Liber Abaci problemów i ukazywanych bardziej wyrafinowanych, zaawansowanych technik obliczeniowych, właśnie ten pozornie prosty ciąg liczbowy odniósł taki „światowy sukces”? Z matematycznego punktu widzenia są to liczby eleganckie i ciekawe, ale nie dlatego przeszły one do historii. Prawdziwy powód ich popularności jest zarówno dziwny, jak i szokujący: liczby Fibonacciego dotyczą nie tylko hodowli królików, ale samej struktury całej naszej rzeczywistości. Są one obecne wszędzie i towarzyszą nam od zawsze, ale jak to często bywa z wielkimi odkryciami, potrzeba bardzo uważnych oczu, aby dostrzec porządek w pozornym chaosie otaczającego nas życia.
Weźmy na przykład słoneczniki i zamiast je po prostu podziwiać, przyjrzyjmy się im dokładniej: zauważymy, jak nasiona układają się w spirale. Ile ich jest? Ot, zwykły słonecznik, policzymy: 34 spiral nasion po jednej stronie i 55 po drugiej. 34 i 55, dwie liczby z ciągu Fibonacciego, czyż nie? Może to zbieg okoliczności, weźmy inny większy słonecznik: 89 i 144 spiral nasion. I jeszcze raz przyjrzyjmy się mniejszemu słonecznikowi: znów 34 i 55 spiral nasion. To niesamowite, ale słoneczniki wydają się rosnąć według ciągu liczb królików Fibonacciego. To tyle? Skądże znowu. Przyjrzawszy się innym kwiatom odkryjemy: 3 płatki w liliach, 5 w dzikich różach, 8 w ostróżce ogrodowej (łac. Delphiniums), 13 w nagietkach. A zastanawialiście się kiedyś dlaczego czterolistna koniczyna stanowi taką rzadkość w przyrodzie? Czy to nie dlatego, że 4 nie jest liczbą Fibonacciego?
Magię ciągu liczb Fibonacciego odnaleźć można w wielu innych miejscach w przyrodzie, zarówno w skali mikro, jak i makro. Oto kilka przykładów: od mikroświata elektronów i kryształów, poprzez widoczny dla naszych oczu świat (kwiaty, szyszki, drzewa, muszle, cyklony), do obiektów makroświata (od orbit planet i księżyców, po sam kształt galaktyk), wszędzie odnajdziemy ten właśnie ciąg liczbowy.
Jest on obecny nie tylko w przyrodzie: stanowi część naszego świata na wszystkich poziomach. Półki w supermarketach, karty do gry, okna, szafki, kalkulatory, pocztówki, karty kredytowe i niezliczone inne otaczające nas przedmioty noszą kształty podyktowane liczbami Fibonacciego – innymi słowy, my, ludzie, lubimy formy, które odpowiadają proporcjom tworzonym przez te liczby. Nie zdajemy sobie z tego sprawy, ale pojęcie piękna kieruje się właśnie tymi liczbami, które badał Fibonacci przy okazji rozmnażania królików, do tego stopnia, że znajdziemy je również w najsłynniejszych dziełach sztuki na świecie. Proporcje pochodzące od tych cudownych liczb ukazują się przed naszymi oczami od wszechczasów: przez piramidy w Gizie po Partenon w starożytności, od Taj Mahal po gmach Organizacji Narodów Zjednoczonych w Nowym Jorku czy wieżę CN w Toronto, zbudowaną w naszych czasach. Piękno w architekturze podąża po prostu za liczbami Fibonacciego. Dotyczy to także piękna w sztuce, sam Leonardo (da Vinci) stosuje proporcje Fibonacciego w swoich najsłynniejszych dziełach, takich jak Mona Lisa, Ostatnia Wieczerza, czy szkic Człowiek witruwiański. Również w muzyce odnajdujemy Fibonacciego i jego liczby, już na poziomie gamy nut, która z czasem przeszła z 5 do 8, aż do naszej nowoczesnej skali chromatycznej 13 nut (!). Wszechobecny ciąg Fibonacciego pojawia się także w samych kompozycjach muzycznych, w strukturze dzieł najsłynniejszych kompozytorów, kształtując muzykę Beethovena, Bacha, Bartóka (a to tylko nazwiska na „b”). W niezliczonych wspaniałych utworach muzycznych liczby Fibonacciego są podstawą harmonii, rytmu, a nawet metrum.
O co w tym wszystkim chodzi? Dlaczego nasza koncepcja piękna zależy od ciągu tych liczb? Nie istnieje jeszcze ostateczna odpowiedź, ale mamy mocną hipotezę. Jeśli otaczająca nas przyroda kieruje się prawami ciągu Fibonacciego, a my jesteśmy przecież częścią natury, to nie ma co się dziwić, że lubimy wszystko, co ma związek z jego cudownymi liczbami. Innymi słowy, jeśli jesteśmy stworzeni z liczb Fibonacciego, to najlepsze ludzkie dzieła, nasza sztuka i nasze piękno opierają się właśnie na nich. Piękno natury i piękno człowieka są tylko pozornie czymś innym, gdyż jeśli przyjrzeć się bliżej, łączą się poprzez tę sekwencję ukazaną przez Fibonacciego na hodowli królików.
Syn średniowiecznych kupców, Leonardo Fibonacci, swoimi liczbami chciał zmienić świat i być może naprawdę mu się to udało.
***
Massimo Marchiori jest profesorem na Uniwersytecie w Padwie (Włochy) i Dyrektorem technicznym European Institute for Science, Media and Democracy (Belgia). Pracował w Narodowym Centrum Badań Holenderskich (CWI), a także w MIT (USA), gdzie przyczynił się do rozwoju licznych światowych standardów dotyczących funkcjonowania sieci. Twórca Hypersearch (prekursor wyszukiwarki Google) i Negapedii (negatywna wersja Wikipedii), zwycięzca licznych nagród, między innymi IBM research award, Lifetime Membership Award od Oxford Society, Microsoft Data Science Award czy MIT TR35 award, nagrody przyznawanej najlepszym innowatorom na świecie.
